La esfera y la cúpula, las formas perfectas para hacer un edificio

La esfera y la cúpula, las formas perfectas para hacer un edificio.  Las formas esféricas son posiblemente la manera más eficiente de construir un edificio. La esfera puede considerarse un circulo en tres dimensiones y matemáticamente es la forma que menos superficie necesita para encerrar un mismo volumen.

Veamos un ejemplo.

Las formas perfectas en la arquitectura son las que derivan de la geometría del círculo

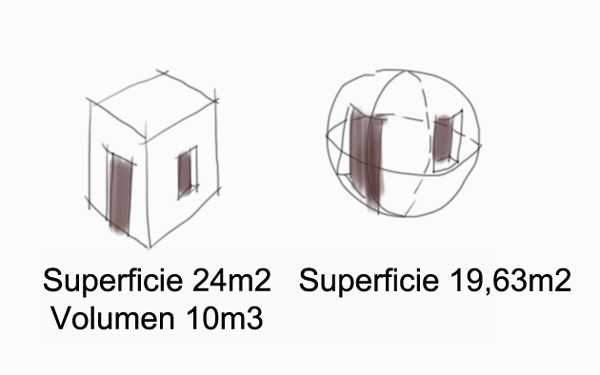
-Un edificio con forma cuadrada de fachadas de lado 2metros de longitud y una altura de 2,5metros  ocupará en planta 4 metros cuadrados y tendrá un volumen de 4 metros cuadrados x 2,5 metros de alto igual a 10 metros cúbicos. La superficie de sus lados es igual a 24metros cuadrados

-El mismo edificio, para que contenga un volumen igual al anterior pero con forma esférica, tendría un radio de 1,58 metros y una superficie de sus lados de 19,63m2, es decir, casi 5metros cuadrados menos de superficie de cerramiento.

Así pues, matemáticamente no hay duda de que una forma esférica es más eficiente que una forma cúbica.  Esto se traduce teóricamente en las siguientes ventajas:

-Desde el punto de vista energético, la esfera tiene menos superficie en contacto con el exterior que un prisma  (19,63 metros cuadrados  frente a 24metros cuadrados), lo que supone menos superficie de pérdida de calor y por lo tanto un abaratamiento en los gastos en calefacción.

-La esfera ocupa menos superficie en planta que una edificación de planta cuadrada por lo que ahorra espacio.

-Estructuralmente las formas en arco funcionan mucho mejor que cualquier otra forma ya que reparten mucho mejor las cargas.

La esfera y la cúpula, las formas perfectas para hacer un edificio.  Y dicho esto, ¿Por qué no construimos todos los edificios con forma esférica?

Si bien teóricamente utilizar la esfera es la mejor manera de optimizar el espacio construido, en la práctica nos encontramos con una realidad muy distinta, ya que el uso de formas esféricas presenta algunos inconvenientes:

-Aunque el espacio ocupado teóricamente por una esfera con el mismo volumen que su equivalente en forma cúbica sea menor, arquitectónicamente no es así, ya que el espacio que vivimos  no es lo mismo que el espacio real calculado con formas matemáticas. La esfera, a efectos de ocupación exterior afecta a un espacio equivalente al volumen de un cubo que la conteniese, por lo que en la práctica no ganaríamos espacio.

-En el interior, las formas curvas impiden poder aprovechar el 100% del volumen, así que nos veríamos obligados a colocar una parte plana y horizontal que inutilizaría parte del volumen de la esfera. Un ejemplo práctico sería un iglú, que se puede considerar media esfera y cuya base es totalmente plana.

-Constructivamente una esfera resulta mucho más compleja de ejecutar que un cubo. Esta complejidad se traduce a un mayor gasto

La esfera y la cúpula, las formas perfectas para hacer un edificio.  Ahora bien, primero la naturaleza y luego el hombre ha sabido adaptar la teoría a la práctica y conseguir soluciones con formas cuasi esféricas  que realmente suponen una mejora considerable frente a su equivalente con otras formas.

-Las colmenas de las abejas. El primer ejemplo y posiblemente el más representativo sea el de la construcción de panales de abejas. Estos pequeños insectos han conseguido la forma casi perfecta: el hexágono. El hexágono, aunque no llega a ser una esfera, se asemeja bastante a ella. La gran ventaja de los hexágonos es que están formados por lados planos que consiguen formar mallas  en plano ilimitadas. (en tres dimensiones no podríamos repetir el hexágono indefinidamente aprovechando a 100% el espacio)

-Los iglúes y las construcciones con forma de cúpula. Una forma de beneficiarse de las formas esféricas es a partir de las cúpulas. Una cúpula es media esfera y por lo tanto, sin llegar a ser 100% eficientes si resultan más eficientes a todos los niveles que su equivalente en una forma prismática.